算法设计与分析报告5 贪心算法
算法设计与分析报告5 贪心算法
本文发布地址(方便阅读):
- https://cmd.dayi.ink/WfnxTsYRQ4OdwI587BGDRQ
- https://blog.dayi.ink/?p=89
- https://www.cnblogs.com/rabbit-dayi/p/17817387.html
- https://type.dayiyi.top
1. 硬币找零问题
贪心
就是假设我们是收银员,需要找零,然后需要选取最少的硬币数量给他人。
我们直接从最大的依次给,给不了就给再小的,很爽。
但贪心的原理是子问题最优解推出整体问题最优解,也就是最优子结构,而对于子问题,只考虑当前怎么做最优,而不考虑整体情况,对于这个我们就只考虑现在需要的硬币而不考虑整体需要多少硬币。
实际的贪心问题需要证明,但是都贪心了,就贪心一点,不要那么多,直接做贪!
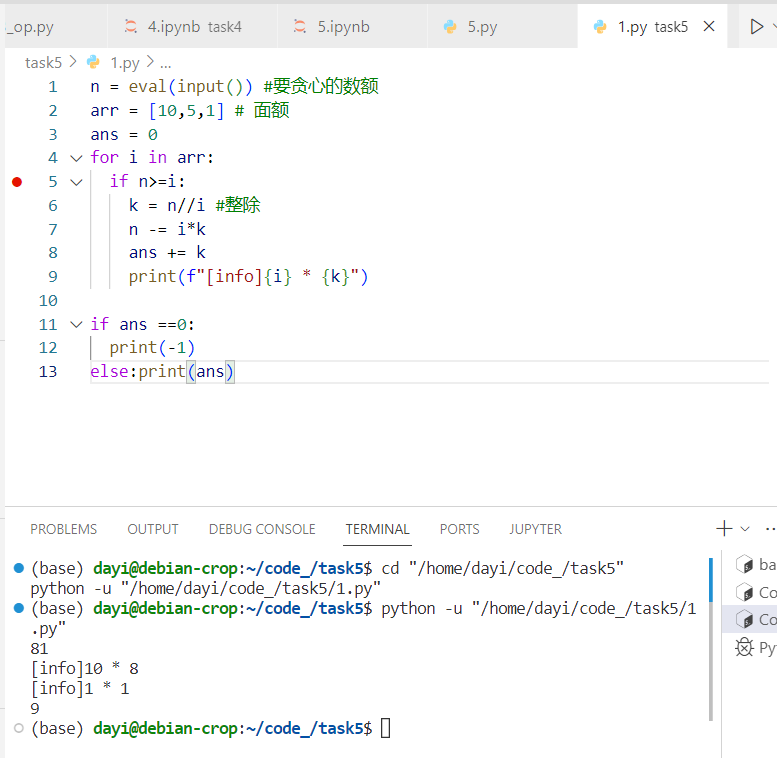
1 | n = eval(input()) #要贪心的数额 |
- 最大面额的硬币比任何其他可能的硬币组合能表示的最大金额还要大。 这意味着任何较大金额的找零都应该首先尽可能多地使用最大面额的硬币
- 较小的硬币面额能被较大的硬币面额整除。
- 组合属性。 对于任意两个硬币面额
a和b,如果a > b,那么对于任何金额x,如果x能够用a来找零,那么x - b也能用a来找零。移除一个较小面额的硬币并不会改变剩余金额能否用较大面额的硬币找零。也就是说,x可以被a整除或者x大于a,那么从x中减去b(得到的金额是x-b)仍然能够使用面额为a的硬币找零。 比如这道题:
https://www.luogu.com.cn/problem/B3635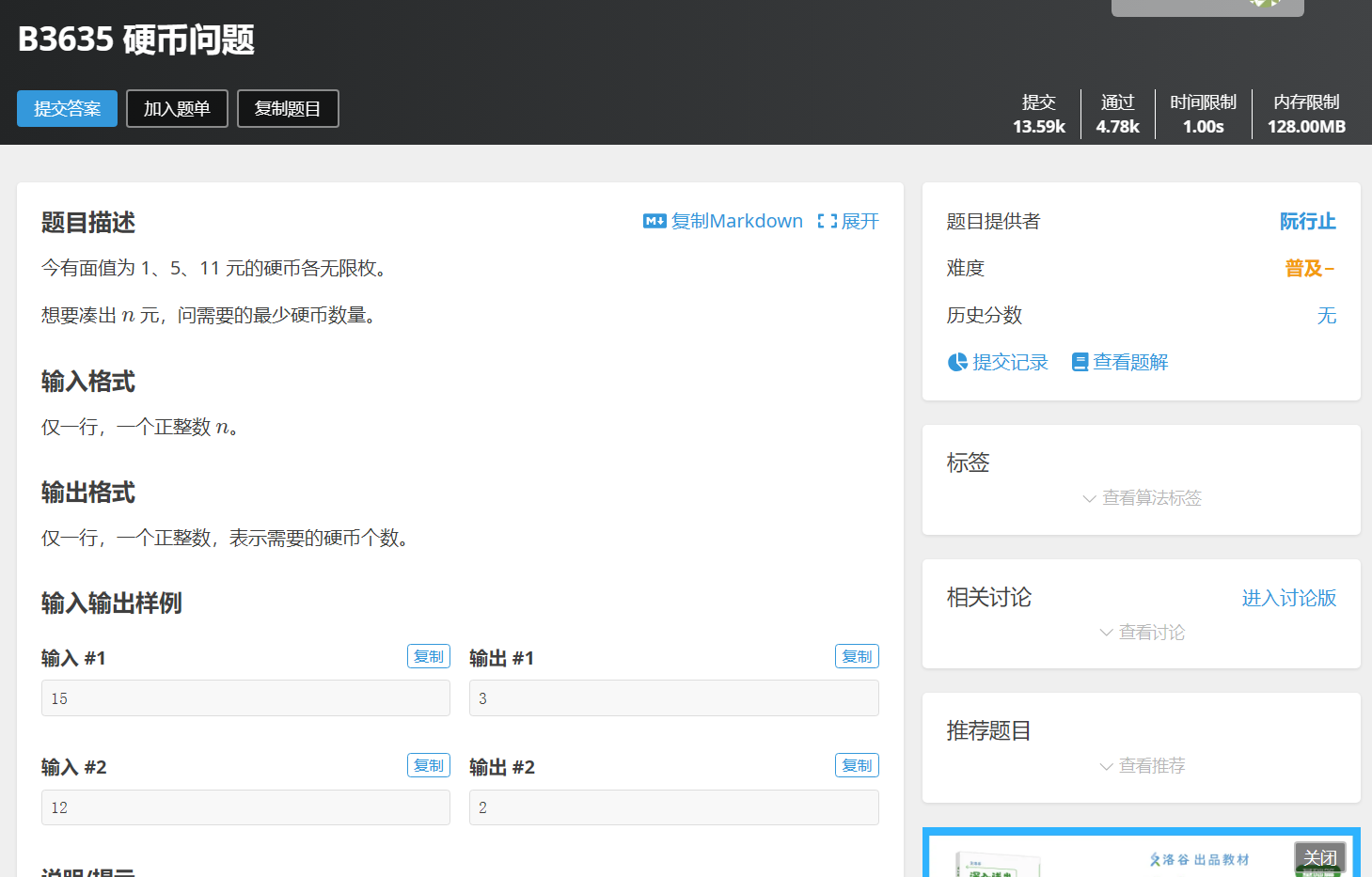
如果我们需要 15 元,我们的贪心算法会这样找:
1 | 15 |
这样就需要5枚硬币,而这里,我们则只需要3枚硬币(3*5)。
一般这两种情况会导致:
- 硬币的面额不能互相组合出更小的面额中的任何一个。
- 较小面额的硬币不能组合成较大面额的硬币。
对于本题中的硬币系统,因为不能保证使用最大面额的硬币后,剩下的金额还能用较小的面额凑出,所以这里不能用贪心算法。
那咋办嘛?
动态规划(Oh no)
定义状态:
dp[i]凑成总金额i所需的最少硬币数量。
假设我们想要凑成金额为6元,那么
dp[6]将包含以下集合:{1, 1, 1, 1, 1, 1}:使用六个1元硬币 1个硬币{1, 5}:使用一个1元和一个5元硬币 2个硬币
状态初始化:
dp[0] = 0,因为凑成总金额0不需要任何硬币。- 其他状态初值可以设为无限,表示还没有找到凑成这个金额的方法。
状态转移方程:
- 要凑成总金额
i,可以通过以下三种方式:- 用一个1元硬币加上金额为
i-1的最优解 - 用一个5元硬币加上金额为
i-5的最优解 - 用一个11元硬币加上金额为
i-11的最优解
- 用一个1元硬币加上金额为
- 因此,状态转移方程为
dp[i] = min(dp[i-1], dp[i-5], dp[i-11]) + 1。
- 要凑成总金额
计算顺序:
- 由小到大计算
dp[i],计算到dp[n]。
- 由小到大计算
结果:
dp[n]
1 | n = eval(input()) |
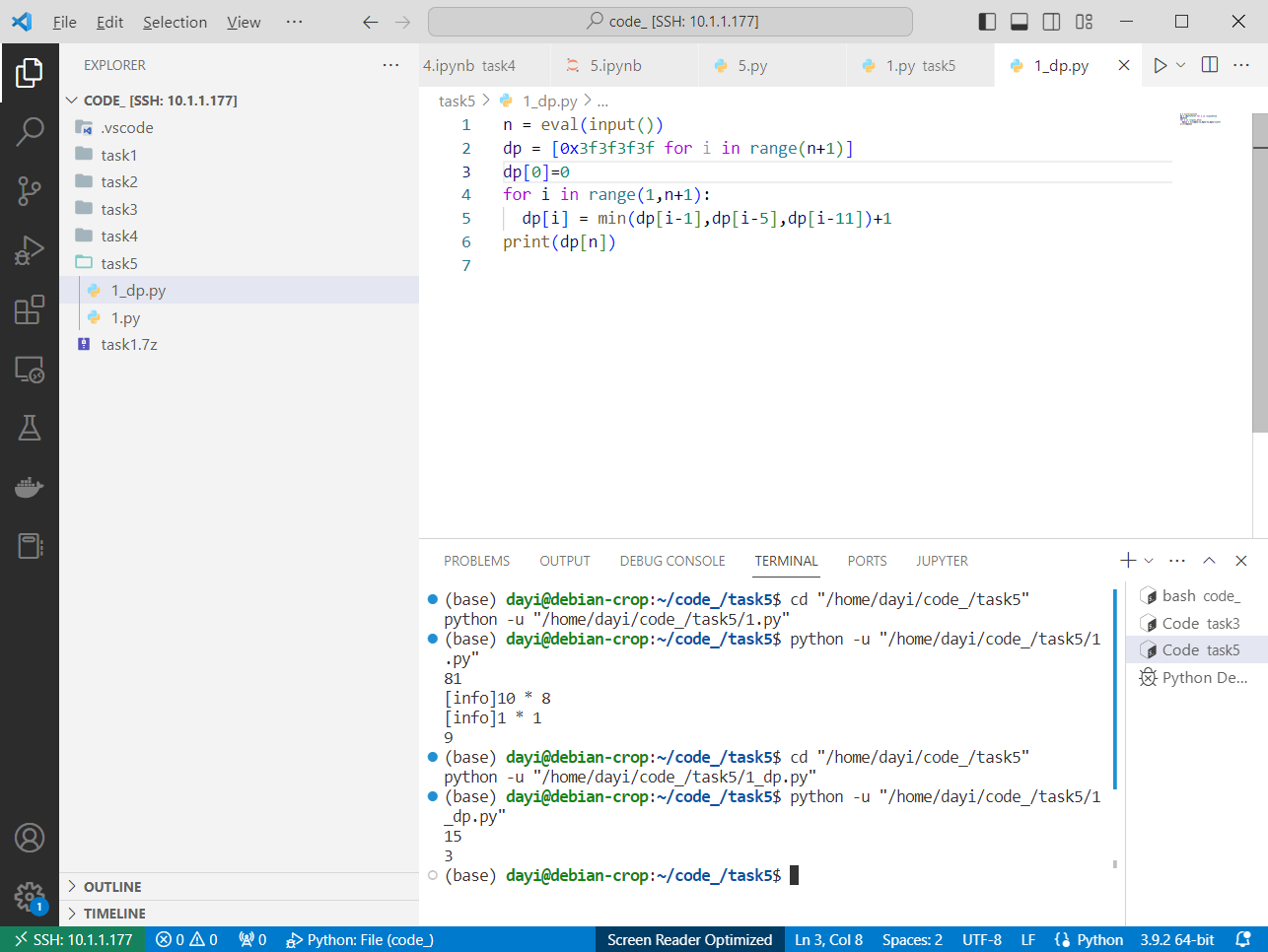
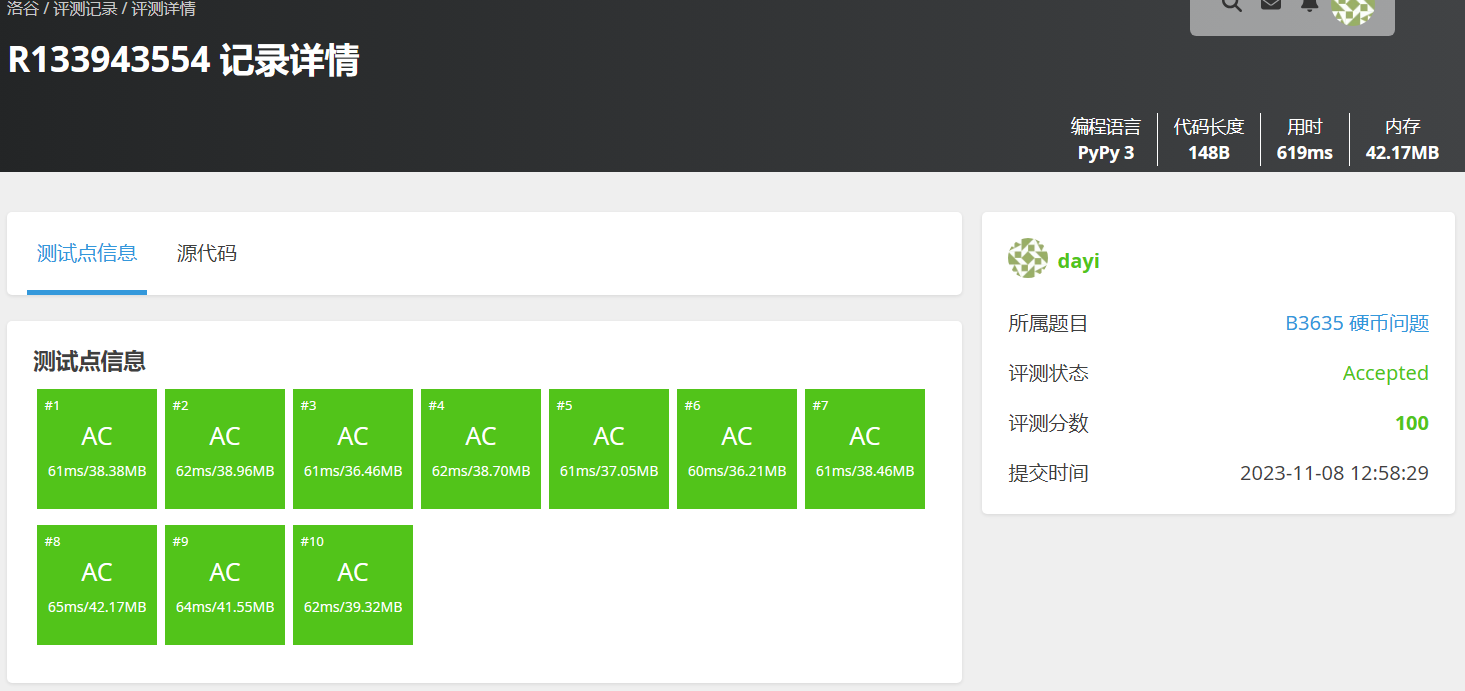
再来一道一样的题目题:
https://vjudge.net/problem/%E8%AE%A1%E8%92%9C%E5%AE%A2-T1781
1 | n,m = map(int,input().split()) |
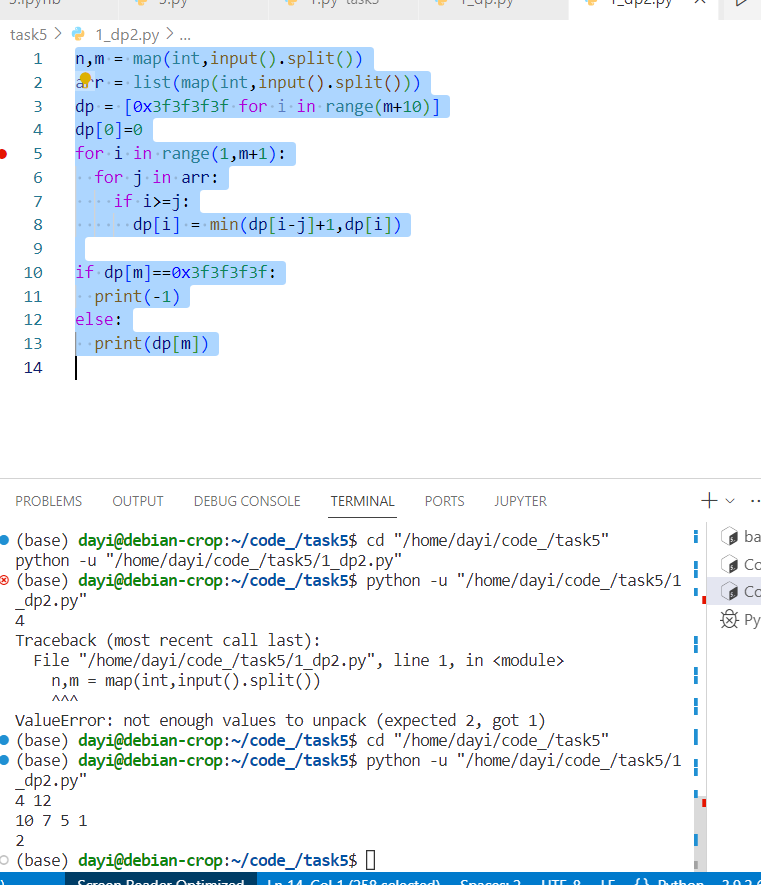
在硬币找零问题中,动态规划提供了一种有效的方式来求解最少硬币数量。较小的金额开始逐步构建解决方案,确保每个子问题都被有效解决。处理具有重叠子问题和最优子结构特点的问题时的优势。与贪心算法相比,DP在此类问题上通常能提供更准确的解决方案,尤其是当问题不能通过局部最优解推导出全局最优解时。

..
AC:
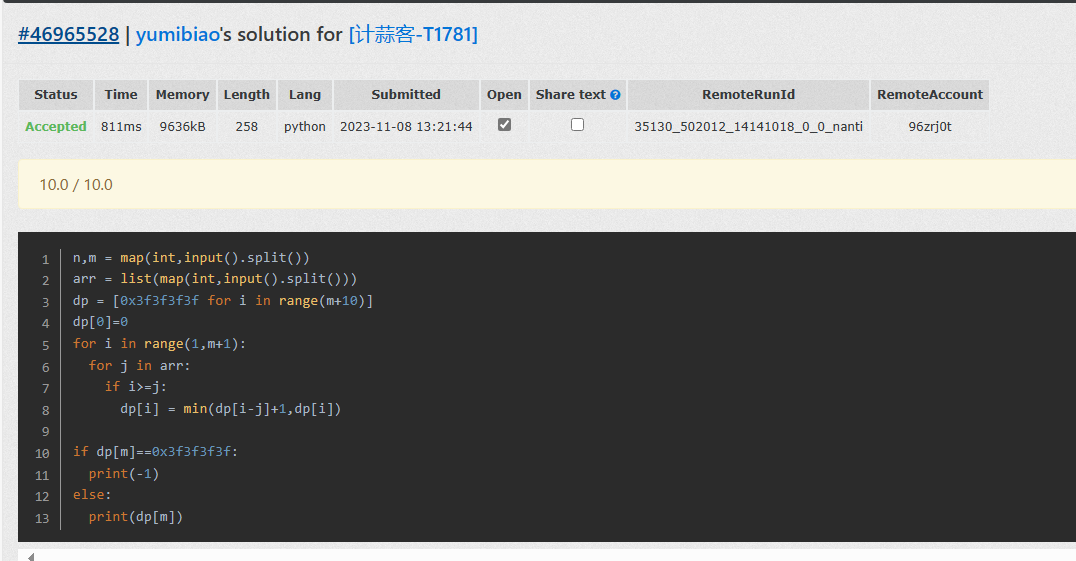
时间复杂度分析
贪心
是$O(K)$,K为硬币的数量!
DP
- 外层循环:遍历从
1到m的所有金额,因此外层循环执行m次。 - 内层循环:对于每个金额
i,遍历所有硬币面额arr[j]。假设硬币的种类数为k,则内层循环执行k次。 - 状态转移:在每次内层循环中,进行了一次
min操作来更新dp[i]。
因此,总的时间复杂度为 $O(m \times k)$,其中 m 是目标金额,k 是硬币种类数。
2.活动安排问题
设有 n 个活动的集合 $E={1,2,..,n}$,其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。
每个活动 i 都有一个要求使用该资源的起始时间 $s_i$ 和一个结束时间 $f_i$,且 $s_i<f_i$。
如果选择了活动 i ,则它在时间区间 $[s_i,f_i)$ 内占用资源。
若区间 $[s_i,f_i)$ 与区间 $[s_j,f_j)$ 不相交,则称活动 i 与活动 j 是相容的。也就是说,当 $f_i≤s_j$ 或 $f_j≤s_i$ 时,活动 i 与活动 j 相容。
选择出由互相兼容的活动组成的最大集合。
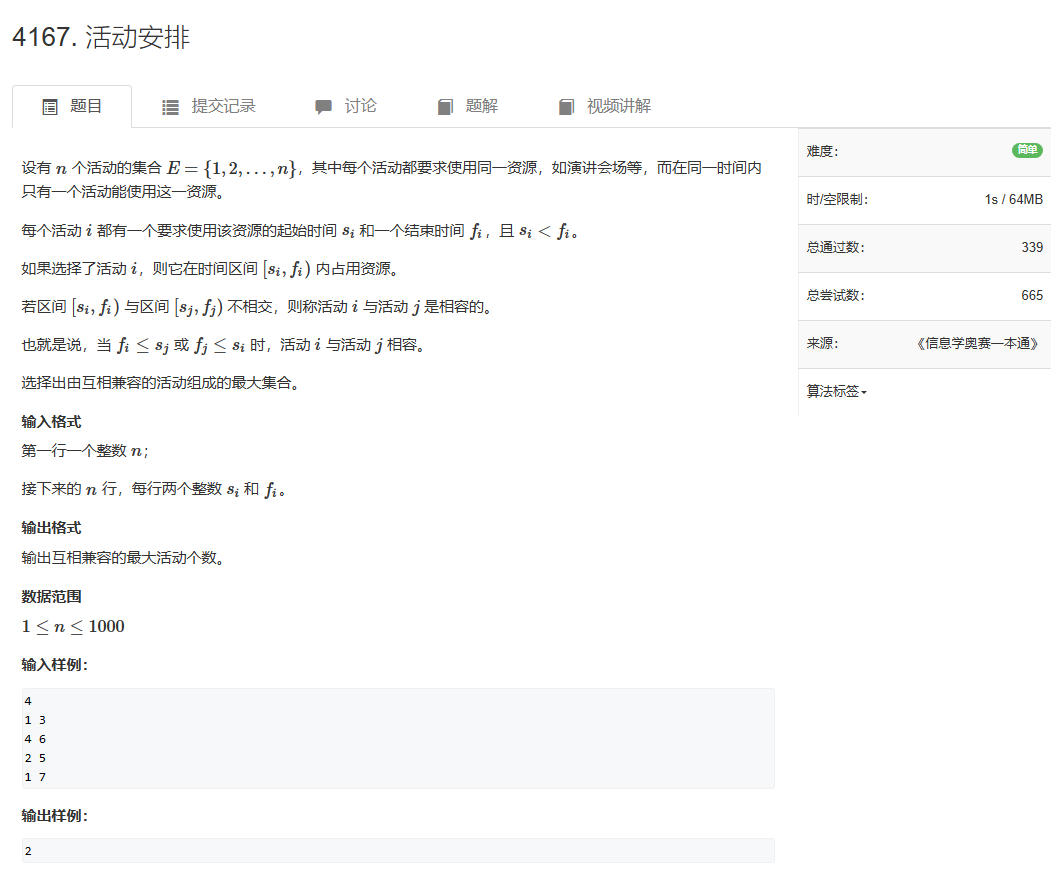
这道题是纯贪心啦(DP也能做):
总是选择结束时间最早的活动,这样留给其它活动的时间就最多了,选择后使得对其他活动影响最小。(证明就不证了)
- 将所有活动按照结束时间进行排序。
- 选择结束时间最早的活动。
- 剔除所有与已选择活动时间上有冲突的活动。
- 重复步骤 2 和 3,直到没有剩余的活动为止。
1 | # 时间复杂度 O(nlogn)(排序) |
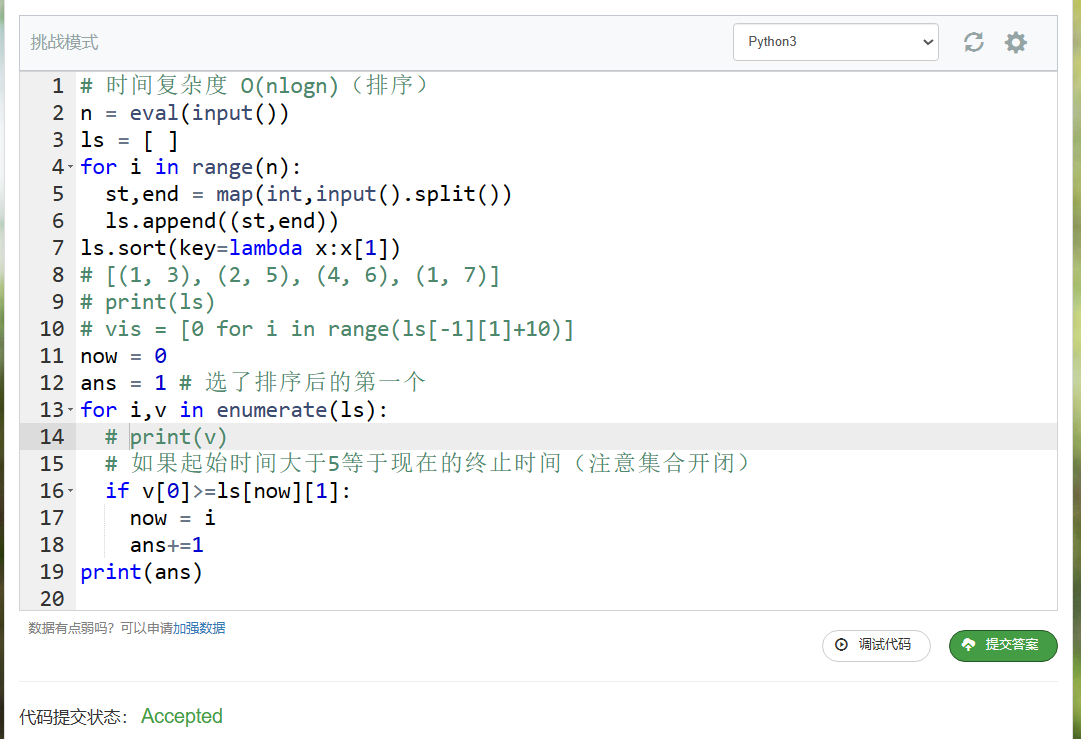
复杂度分析
活动按结束时间排序和贪心选择过程。
活动排序:通常,排序算法的时间复杂度为 $O(n \log n)$,其中 $n$ 是活动的数量。
贪心选择过程:在排序后的活动列表中,贪心算法从第一个活动开始,依次检查每个活动是否与已选择的活动相容。这一过程的时间复杂度为 $O(n)$,因为每个活动最多被检查一次。
选择活动:对于每个活动,检查是否与已选择的活动冲突是常数时间的操作,因此不会增加时间复杂度。
总时间复杂度:总的时间复杂度为排序时间复杂度和贪心选择过程的时间复杂度之和,即 $O(n \log n) + O(n) = O(n \log n)$。
额外空间:贪心算法除了存储活动列表外,只需要常数个额外变量(如记录当前活动的结束时间等),因此空间复杂度为 $O(n)$,其中 $n$ 是活动列表的大小。
3.背包问题
- 因为完全背包和01背包都在之前的实验里有啦
- 这里就拿这两种问题下的和课本样例输出下
f[i][j]数组吧!
01 背包
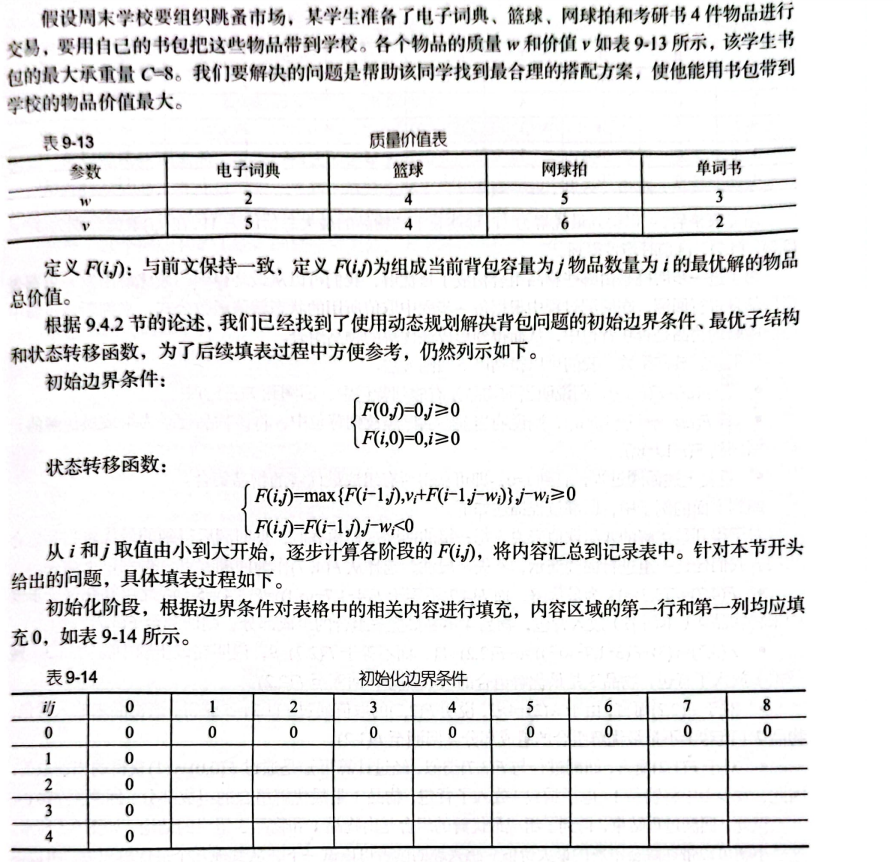
1 | n,c= 4,8 |
1 | # 01背包 |
1 | 0 0 0 0 0 0 0 0 0 |
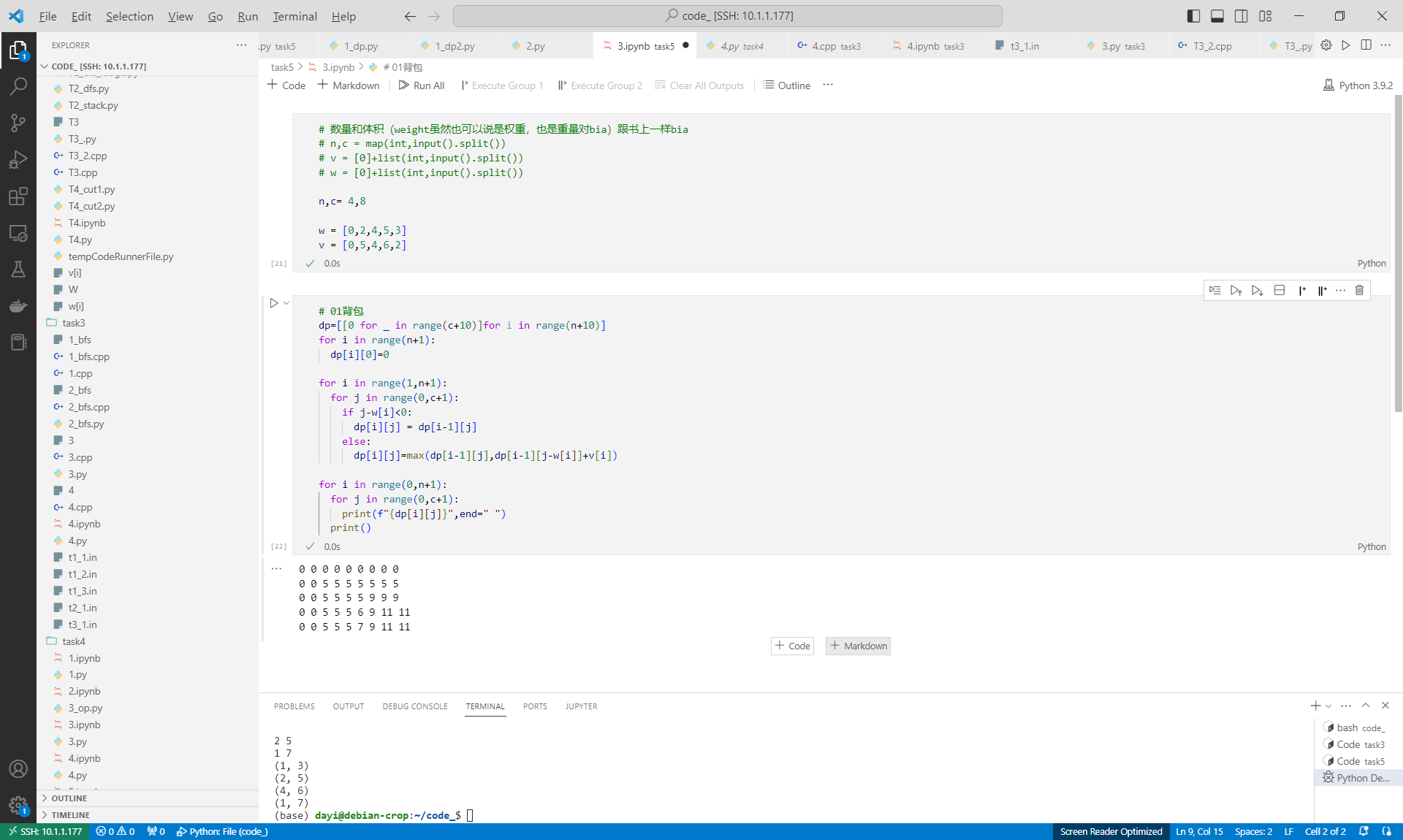
回溯选择了什么:
1 | # 回溯找出选中的物品 |
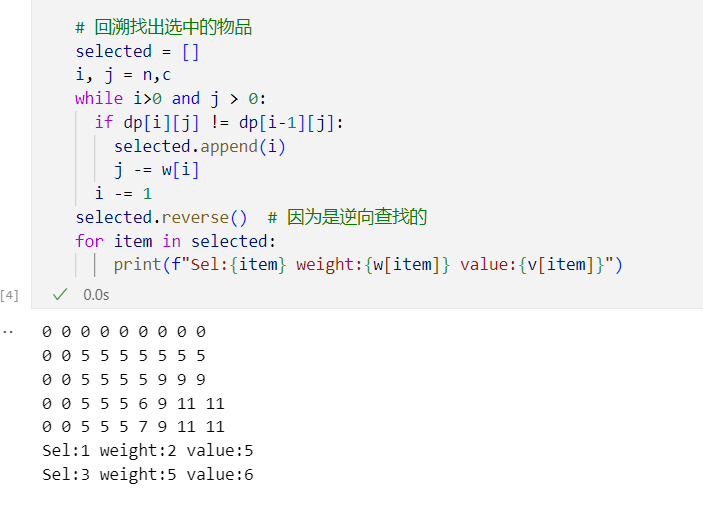
贪心?
我觉得是不对的啦
至少不一定可以求出最优解,贪心算法在每一步都选取当前最优的选择,但是对于01背包问题,当前最优的选择不一定能导致全局最优解。
就比如这样,假设背包的容量为10,有以下三件物品:
- 物品A:重量3,价值5
- 物品B:重量4,价值6
- 物品C:重量7,价值10
如果使用贪心算法根据单位重量价值(价值除以重量)来选择物品,我们将会选择物品 A(单位重量价值为 1.67)和物品 B(单位重量价值为1.5),总重量为 7,总价值为 11。
但是,最优解是选择物品 B 和物品 C,总重量为 11(如果背包可以装 11 的话),总价值为16。
但是课本例题的数据如果用这种贪心似乎还能跟DP选的一样,但这不能全部情况啦
1 | n,c= 4,8 |
输出结果,虽然跟 01 DP 一样,但是这个题目正确不能说明对于全部正确。
1 | Sel:1 weight:2 value:5 attempt:2.5 |
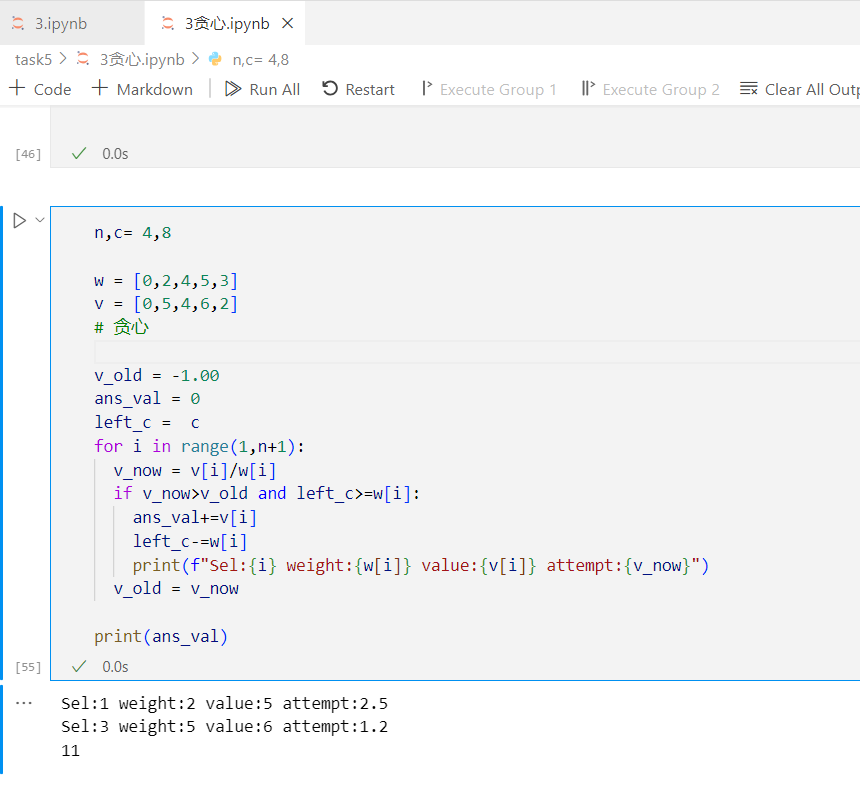
比如这样一组数据就没法正常贪心成功:

所以贪心不能代表全部,也经常不能得出正确解(不如说得出正确解是巧合)
完全背包
假设背包容量还是这个情况($C=8$),但是我们的物品有无限个。

这里数据比较小,没有用递推优化 DP
1 | # 完全背包 |

1 | 0 0 0 0 0 0 0 0 0 |
可以贪心的分数背包
讲真,我是第一次见这种背包。
问题描述
【问题描述】设有编号为1、2、…、n的n个物品,它们的重量分别为$w_1、w_2、…、w_n$,价值分别为$v_1、v_2、…、v_n$,其中$w_i、v_i$(1≤i≤n)均为正数。
有一个背包可以携带的最大重量不超过W。求解目标:在不超过背包负重的前提下,使背包装入的总价值最大(即效益最大化),与0/1背包问题的区别是,这里的每个物品可以取一部分装入背包。
问题
在这个分数背包问题中,我们可以通过贪心算法来解决。因为每个物品可以只取一部分,所以我们可以按照物品的单位重量价值(即价值与重量的比值)进行排序,优先选择单位重量价值最高的物品装入背包,直到背包无法再装更多的物品。
$把一个物品变成w_i个单位,每个单位x_i收益不就行了,每个重量是1,这样就是取W个最大的显然就是对滴$
- 计算每个物品的单位重量价值。
- 按照单位重量价值降序排列所有物品。
- 遍历排序后的物品列表,依次尝试将每个物品装入背包,直到背包的容量达到限制。
这个代码首先计算了每个物品的单位重量价值,并按照这个价值进行排序。然后,它遍历这个排序后的列表,尽可能地将物品装入背包,直到背包装不下更多的物品为止。
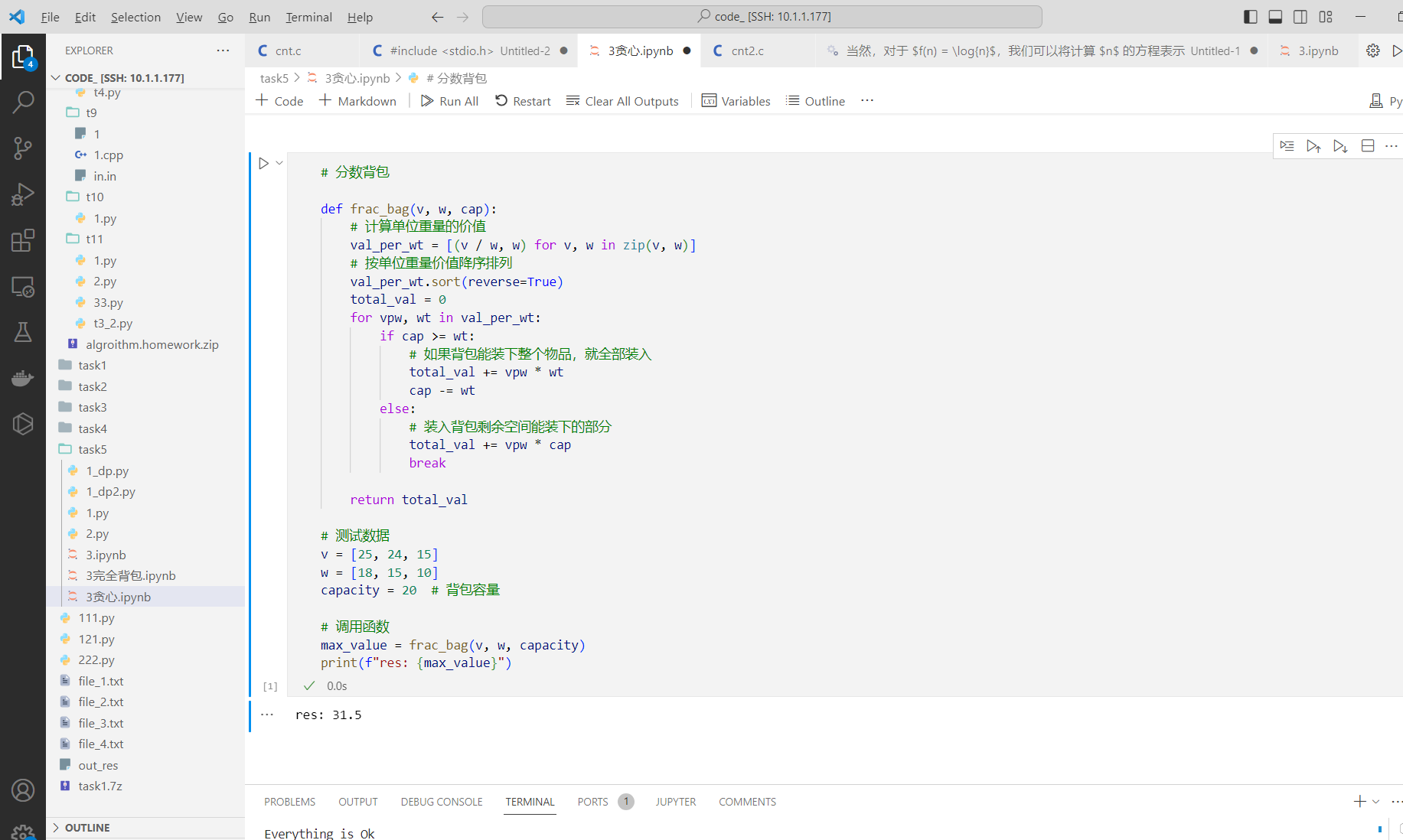
代码
1 | # 分数背包 |
时间复杂度分析
- 计算单位重量价值:$O(n)$,其中 $n$ 是物品的数量。
- 排序:$O(n \log n)$,最耗时的步骤。
- 遍历并装入背包:$O(n)$。
总体时间复杂度为 $O(n \log n)$。
二、总结
贪心算法在解决特定类型的问题时表现出显著的效率和简洁性,尤其是在硬币找零、活动安排、背包问题等领域。这些问题展示了贪心算法的核心特点:局部最优选择能够导致全局最优解。
硬币找零问题:当硬币系统满足特定的条件时,贪心算法能够有效地找到最少硬币数量的解决方案。但在一些情况下,这种方法可能无法提供最优解,此时可以使用动态规划来确保找到全局最优解。
活动安排问题:通过选择结束时间最早的活动,我们能够构建出最大的相容活动集合。
背包问题:
- 对于01背包问题,我们发现贪心算法并不总是能找到最优解,尤其是当物品不能被完全分割时。动态规划在这种情况下提供了一个更可靠的解决方案。
- 在完全背包问题中,动态规划同样表现出其适应性和效率,能够处理每种物品数量无限的情况。
- 对于分数背包问题,贪心算法再次显示了其效能,因为物品可以部分取用,使得按单位价值排序后的贪心选择成为一个有效的策略。
贪心算法在许多问题中都是一个有用且高效的工具,特别是在问题的结构允许通过局部最优选择来达到全局最优时。但,它并不总是能提供最优解,这就需要根据问题的具体性质来选择合适的算法,如动态规划等。在算法设计与分析中,理解问题的本质及其约束条件对于选择正确的解决方案至关重要。