算法实验报告2
算法实验报告2
本文链接:
- https://type.dayiyi.top/index.php/archives/231/
- https://www.cnblogs.com/rabbit-dayi/articles/17864571.html
- https://cmd.dayi.ink/cbNEvd5MTn-YQFw0J7IuKw?edit
- https://blog.dayi.ink/?p=155
1.求幂集问题
也就是求全部的组合
DFS
把全排列 DFS 树给记录下来就可以
DFS 到每个节点的时候,记录当前状态加入到结果集即可。
复杂度$O(2^{N})$
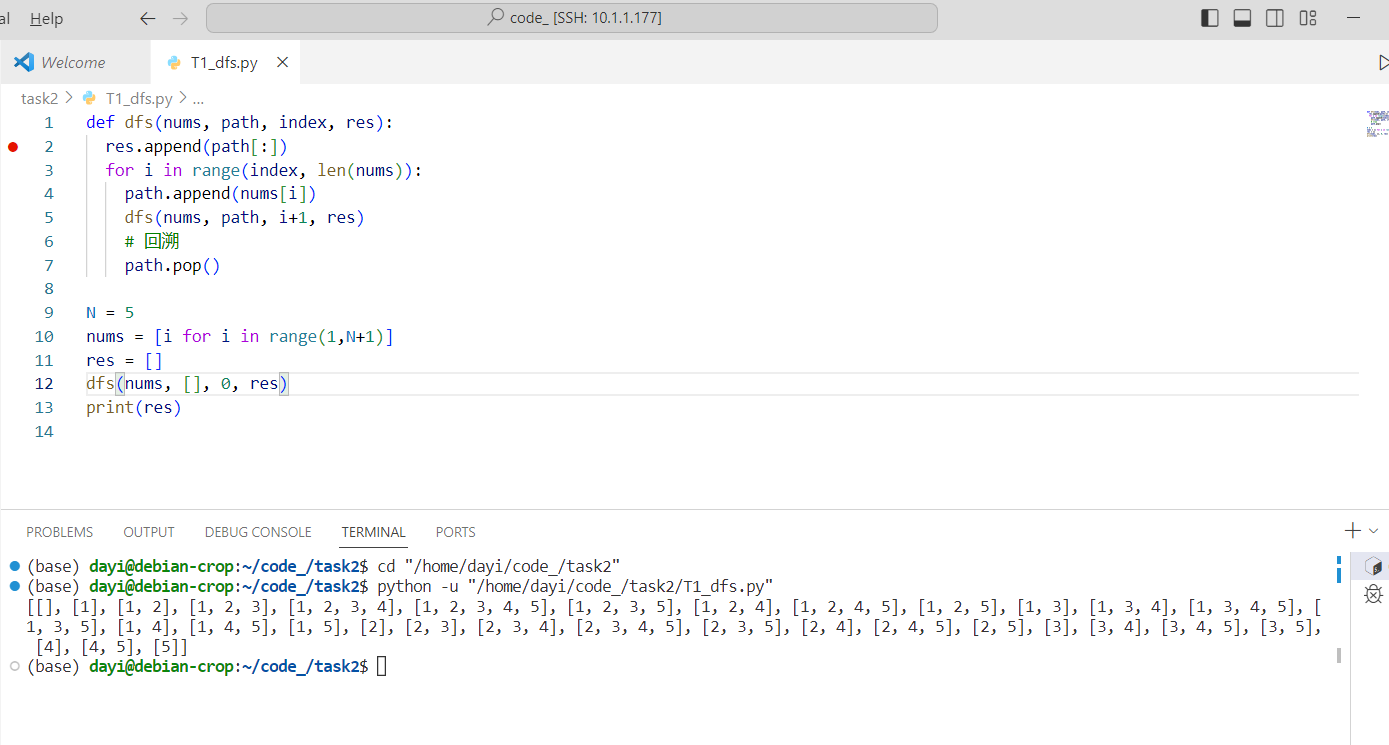
Python 代码:
1 | def dfs(nums, path, index, res): |
位运算
位运算
- 复杂度$O(N*2^n)$
- 假设有 5 个物品,每个物品可以选或者不选。
0 0 0 0 0: 5个二进制,1表示选,0表示不选- 这样下来,
2^5次方就可以把全部的情况枚举出来。 - 整数 0 的二进制表示
00000对应空集。 - 整数 1 的二进制表示
00001对应只含有第一个元素的子集。 - 整数 2 的二进制表示
00010对应只含有第二个元素的子集。 - …以此类推…
- 整数 31 的二进制表示
11111对应包含所有五个元素的集合本身。 - 这样下来,每个数都是一个子集,求完即可。
- 每一个从 $0$ 到 $2^n - 1$ 的整数都对应一个唯一的子集。对于每个整数,检查其二进制表示中的每一位,如果当前位是
1,表示选中,当前位是0,便不选。
落实到具体操作上:
- 位操作符
& i是当前数(1 << j)把1左移j次- i = 01000
- j = 1<<4 = 0100
i & j= 1
如果 i & j = 1 则说明当前位是1,选中当前的元素。
1 | N = 15 |

时间复杂度
深度优先搜索(DFS)
- 在DFS方法中,我们从空集开始,逐步添加元素,直到遍历完所有元素。
- 每到达一个新节点时,当前路径的一个副本被添加到结果集中。
- 对于每个元素,都有选择和不选择两种可能,这导致了总共有 $2^N$ 种可能的组合(幂集),其中 $N$ 是数组中的元素数量
- 虽然这里是递归,但递归深度和每层递归的工作量都是有限的,因此时间复杂度不是阶乘级别的。
位运算
对于每个整数,我们检查其二进制表示的每一位,以确定是否包括数组中对应位置的元素。
对于每个子集,我们需要检查 $N$ 位以确定哪些元素被包括在内。因此,总的时间复杂度是 $O(N \times 2^N)$,其中每个子集需要 $O(N)$ 来构建。
OVO
- DFS 方法的时间复杂度是 $O(2^N)$,而位运算方法的时间复杂度是 $O(N \times 2^N)$。
- 由于 $N \times 2^N$ 和 $2^N$ 之间的差异通常不是非常大(尤其是对于小型到中型的数据集),在实践中的性能差异可能不会很明显。
2.N皇后问题 实现回溯法求解皇后问题递归和非递归框架
N 皇后,在 N×N 的棋盘上放置 N 个皇后,使得它们不能相互攻击,即任何两个皇后都不能处在同一行、同一列或同一对角线上。
- 枚举每个点
- 检查当前的点是否可以放置皇后
检查函数
- 行
- 列
- 斜行
落实到具体操作上:
因为一个行 一个列 一个斜行 只能放置一个皇后
直接标记当前行列是否可以放置皇后。
- 对于每一行 一个数组
row[N] - 对于每一列 一个数组
col[N] - 对于每一斜行
- 对角线
- 反对角线
对于对角线来说
- 每条直线可以表示为:$y = -x+b$
- 截距:$b = y+x$
- 每个截距可以表示一条对角线
- 根据取值,于是,对于每个单元$(x,y)$的对角线,就可以
dg[y+x]来进行表示。
而对于反对角线来说
同样的:
- 每条直线可以表示为:$y = x+b$
- 截距:$b = y-x$
- 每个截距可以表示一条对角线
- 根据取值,于是,对于每个单元 $(x,y)$ 的对角线,就可以
adg[y-x]来进行表示。
但是根据定义域来说,$x+y$ 可能为负数,对于计算机来说,可能会导致数组越界。而我们只需要表示当前行是否被占,直接对于每个数 +N 即可。
也就是用adg[y-x+N]来表示 $(x,y)$ 的对角线有没有被占。
综上
- 行
row[x](如果DFS按照这个顺序枚举,其实不需要添加) - 列
col[y] - 对角线
adg[y+x] - 反对角线
adg[y-x+N]
检查函数可以这样写:
1 | row = [0 for i in range(n+10)] |
对于放置函数,其实就是标注一下,但是这样可以提升写代码的幸福感。
1 | def place(x,y): |
DFS 搜
- 时间复杂度$O(n!)$
简单写一下:
1 | # 检查当前位置是否可以放置 |

带结果打印:
1 | # 检查当前位置是否可以放置 |
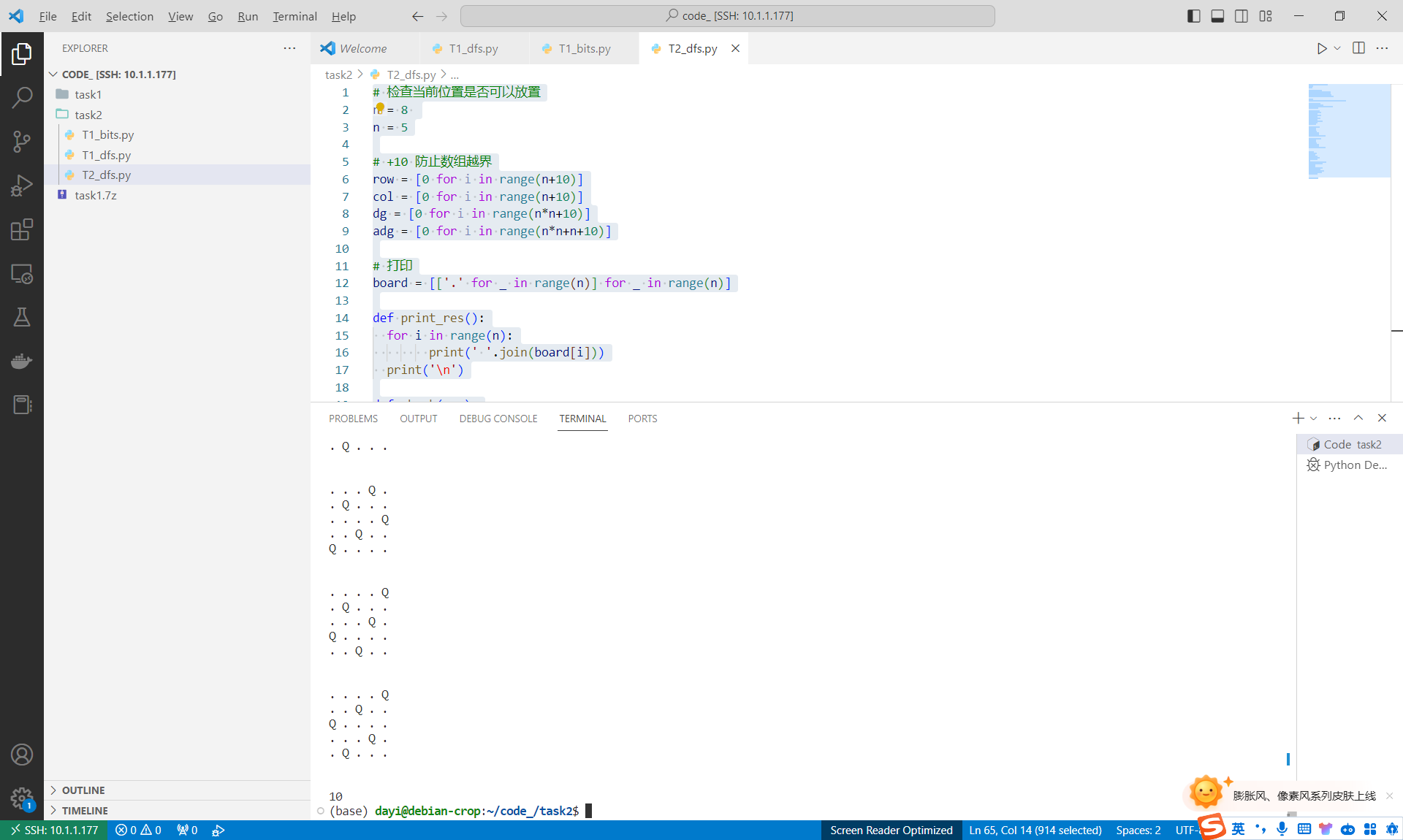
1 | # 检查当前位置是否可以放置 |
TLE了,但是我觉得python已经很快了。
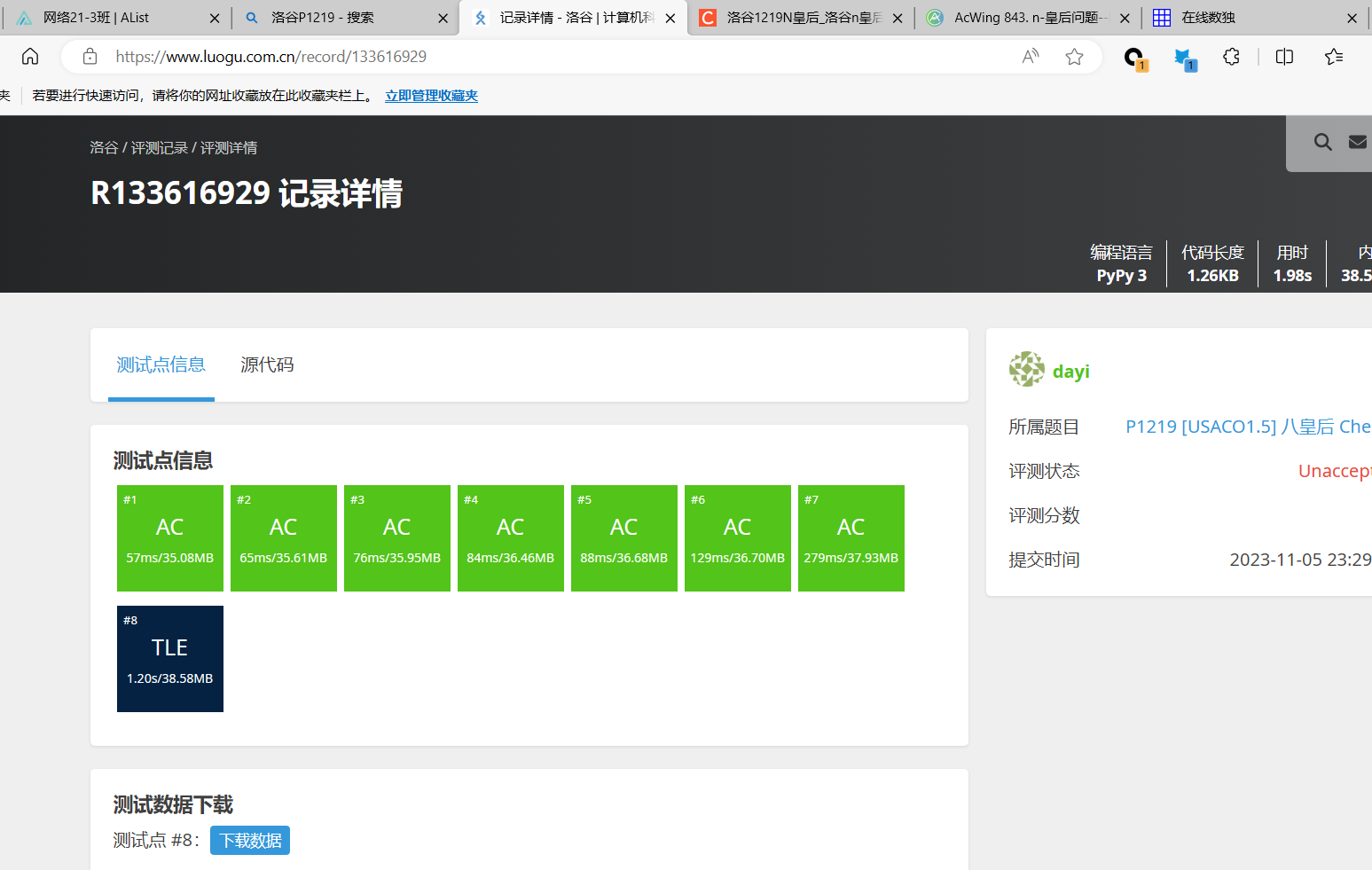
非递归
用栈模拟的,我实在没想到怎么用
1 | # 初始化棋盘参数 |
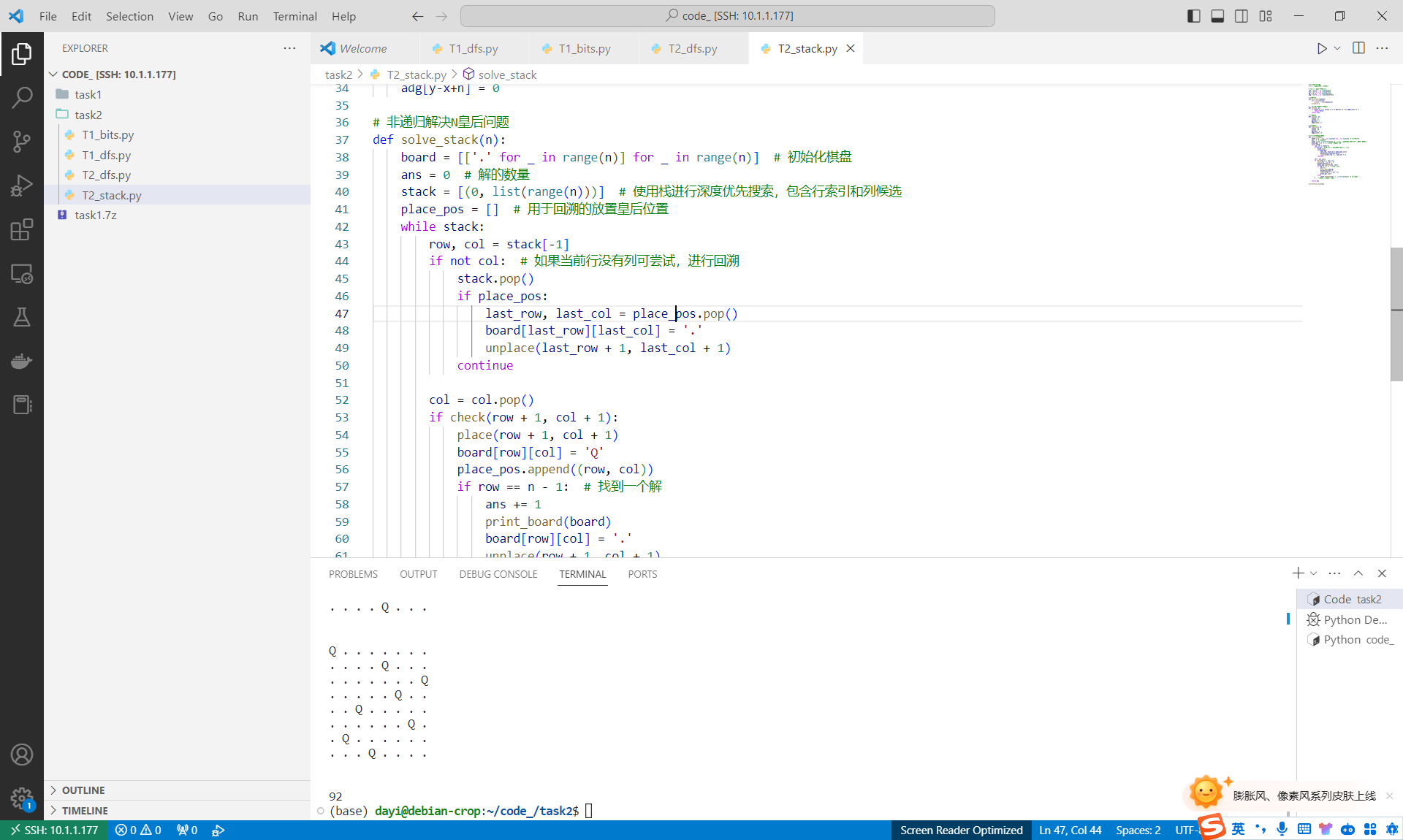
时间复杂度
尽管看起来像是 $O(N!)$ 的复杂度(每行选择一个位置,共有 $N$ 行),实际上由于皇后的约束条件(不能在同行、同列、同对角线上),并不是每行都有 N 个可选位置。事实上,随着递归的深入,可选位置的数量迅速减少。平均情况下的时间复杂度近似于 $O(N!)$,但实际上通常会更低。
非递归回溯的时间复杂度与递归方法相似,也近似于 $O(N!)$。在非递归方法中,栈的使用取代了递归调用的栈帧,但算法的基本操作和约束条件检查相同,因此时间复杂度保持不变。
两种方法的时间复杂度都近似于 $O(N!)$,但实际执行效率通常会更高,因为皇后的约束条件大幅减少了实际的搜索空间。
3. 01包问题
这个,讲真如果第一次学 DP 的话,肯定会有点难理解。
问题
有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
第 $i$ 件物品的体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
爆搜,对于每个物品进行枚举一次
这个方案如 T1 的枚举,时间复杂度是 $O(N!)$ 或者 $O(2^N*N)$
当 $N > 20$ 的时候,肯定是搜不动了。
因此当 $N = 1000$ 的时候,该方案应该是不可取的。
DP
状态属性
- 状态表示:
f[i][j] - 集合:装了前 i 个物品,总体积不超过 j 的选法的集合
- 属性:$max$ 值
状态转移
对于第 $i$ 个物品,可以选择装或者不装。
- 我不打算装这个物品
我的体积不需要被消耗。
我的最大的值没有变,可以直接对 f[i-1][j] 进行状态转移。
得到 $f[i][j] = f[i-1][j]$ ,结束。
我打算装这个物品:
- 我需要
w[i]的空间 - 我能获得的价值是
v[i] - 当前我一定要装这个物品,一定要花费
w[i]的空间(重量) - 我装完之后的背包重量不能大于j
于是我的状态转移方程:
$f[i][j] = f[i-1][j-w[i]]+v[i]$
- 我需要
两种情况都可能会影响到后续的结果,因此,需要将两个值合并为一个状态(`f[i][j]``)
- $f[i][j]$的属性是MAX,直到最后,我只要出现过的最大值,如果当前的值小于$f[i-1][j]$的值
- 也就是如果
- $f[i-1][j]=10$
- $f[i-1][j-w[i]]+v[i]= 9$ (假设)
- 我$f[i][j]$ 应该等于10
- $f[i][j]$的属性是MAX,直到最后,我只要出现过的最大值,如果当前的值小于$f[i-1][j]$的值
最后的状态转移方程为:
$f[i][j] = \max{f[i-1][j],f[i-1][j-w[i]]+v[i]}$
(截个图防止公式坏掉)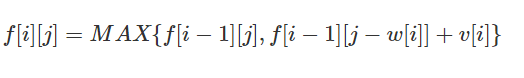
对于最终的结果显然就是:
$dp[N][W]$ 这个值是前 N 个物品,重量小于等于 W 的背包可以获得的最大值
对于处理的过程,要注意:
- $j-w[i]$ 应该大于 0,背包空间如果小于 0 肯定不太合理,也会数组越界
然后直接去写代码就好啦
1 |
|
通过测试: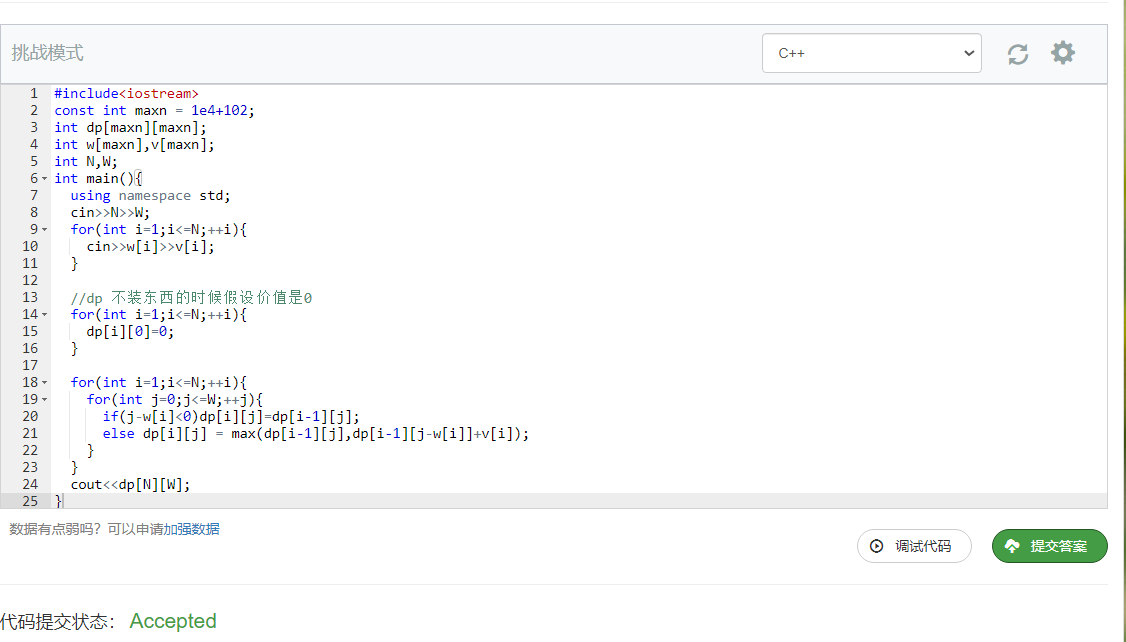
压缩下数组
- 你会发现,我们的状态
dp[i][j]只会从:dp[i-1][j]dp[i-1][j-w[i]]
- 这两个状态转移过来
- 也就是说之前的状态与最终答案和当前计算的状态没有关系
- 即 $dp[i][j]$ 只依赖于 $dp[i-1][j]$ 和 $dp[i-1][j-w[i]]$
动态规划状态压缩的核心在于识别出状态转移仅依赖于有限的几个状态。
但是注意:
- 我们只关心 “当前” 和 “上一个” 两个状态,这样就可以只用一个一维数组啦。
- 但是为了确保 “当前状态” 是基于 “上一个状态” 计算的,需要须反向遍历背包容量(重量)。
- 因为如果正向遍历,当计算到 $dp[j]$ 时,$dp[j-w[i]]$ 可能已经在这一轮循环中更新过了,使用这一轮的信息而不是上一轮的信息。
压缩后的状态转移方程为:
$$
dp[j] = \max{dp[j], dp[j-w[i]] + v[i]}
$$
dp[j]表示在不超过重量j的前提下,目前为止能得到的最大价值。dp[j-w[i]] + v[i]表示如果你选择放入第i个物品,那么背包中剩余的重量就是j-w[i],对应的最大价值就是dp[j-w[i]],加上第i个物品的价值v[i]=dp[j-w[i]] + v[i]。
对于状态转移:
- 不放第
i个物品时,背包的最大价值(即dp[j])。 - 放入第
i个物品时,背包的最大价值(即dp[j-w[i]] + v[i])。
然后取这两种情况的 $max$ 作为新的 dp[j] 的值。
最后:dp[W] 就是小于W能获得的最大价值。
每次计算 dp[j] 时,dp[j-w[i]] 保持的是上一个物品状态的值。
dp[j-w[i]] 是基于第 i-1 个物品时的最大价值
如果正序遍历,那么在计算较大的 j 值时,可能会重复计算某个物品的价值。
OK
这样代码如下:
1 |
|
空间复杂度从 $O(NW)$ 降低到了 $O(W)$,其实这里读入的数组的时候可以直接算dp方程,还能再省,但是一般空间不会不够用。
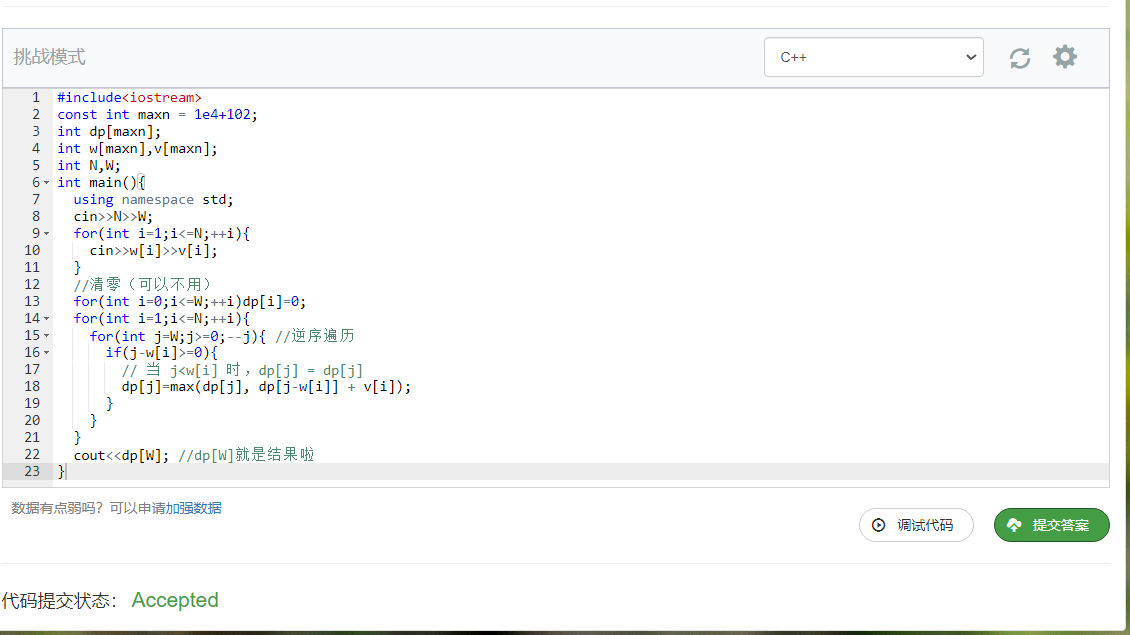
然后写个python的版本
1 | maxn = 1000+101 |
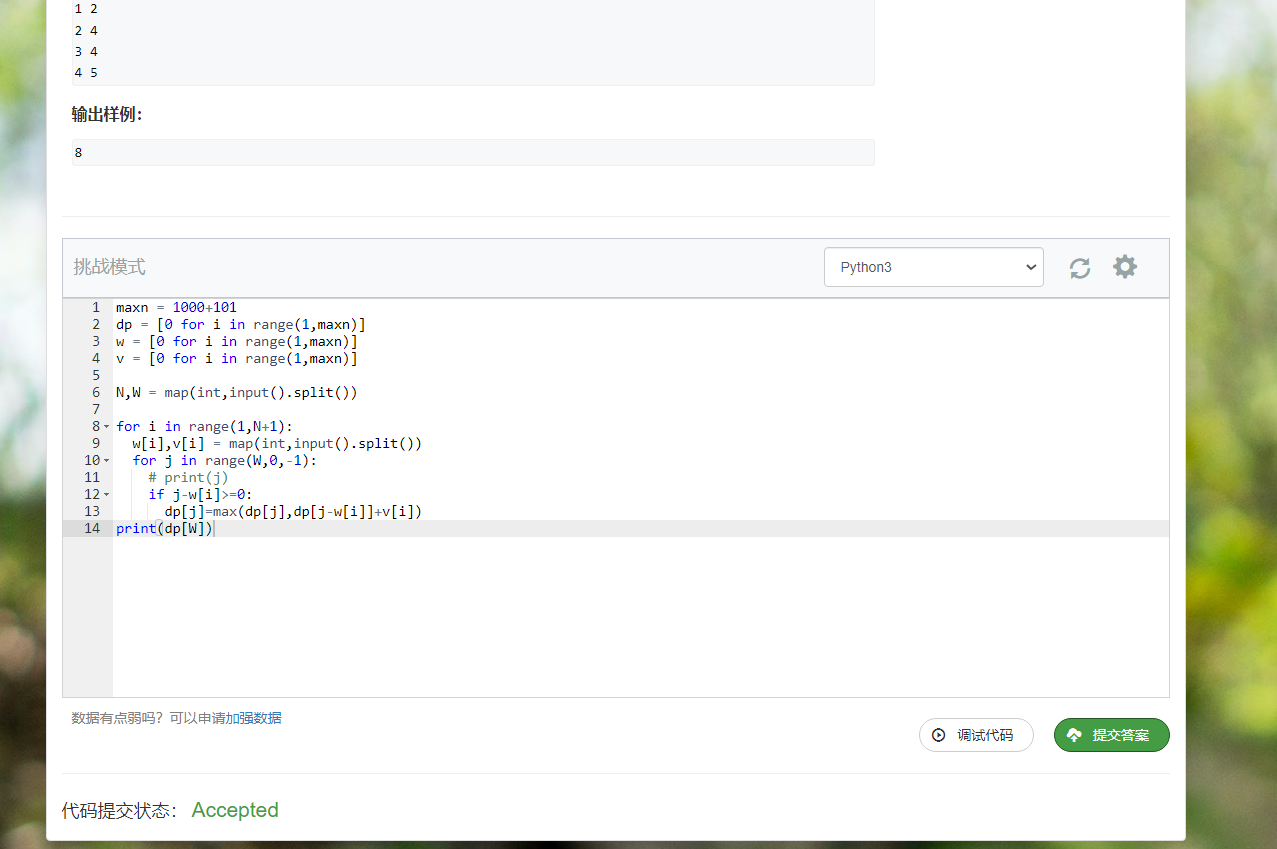
时间复杂度
其实很简单啦,这里遍历$NW$,所以时间复杂度$O(NW)$
所以这里就很明显了。
4.数独问题
你需要把一个 9×9 的数独补充完整,使得数独中每行、每列、每个 3×3 的九宫格内数字 1∼9均恰好出现一次。
可以直接拿一道题过来:
https://vjudge.net/problem/POJ-3074#author=GPT_zh
https://www.acwing.com/problem/content/description/168/
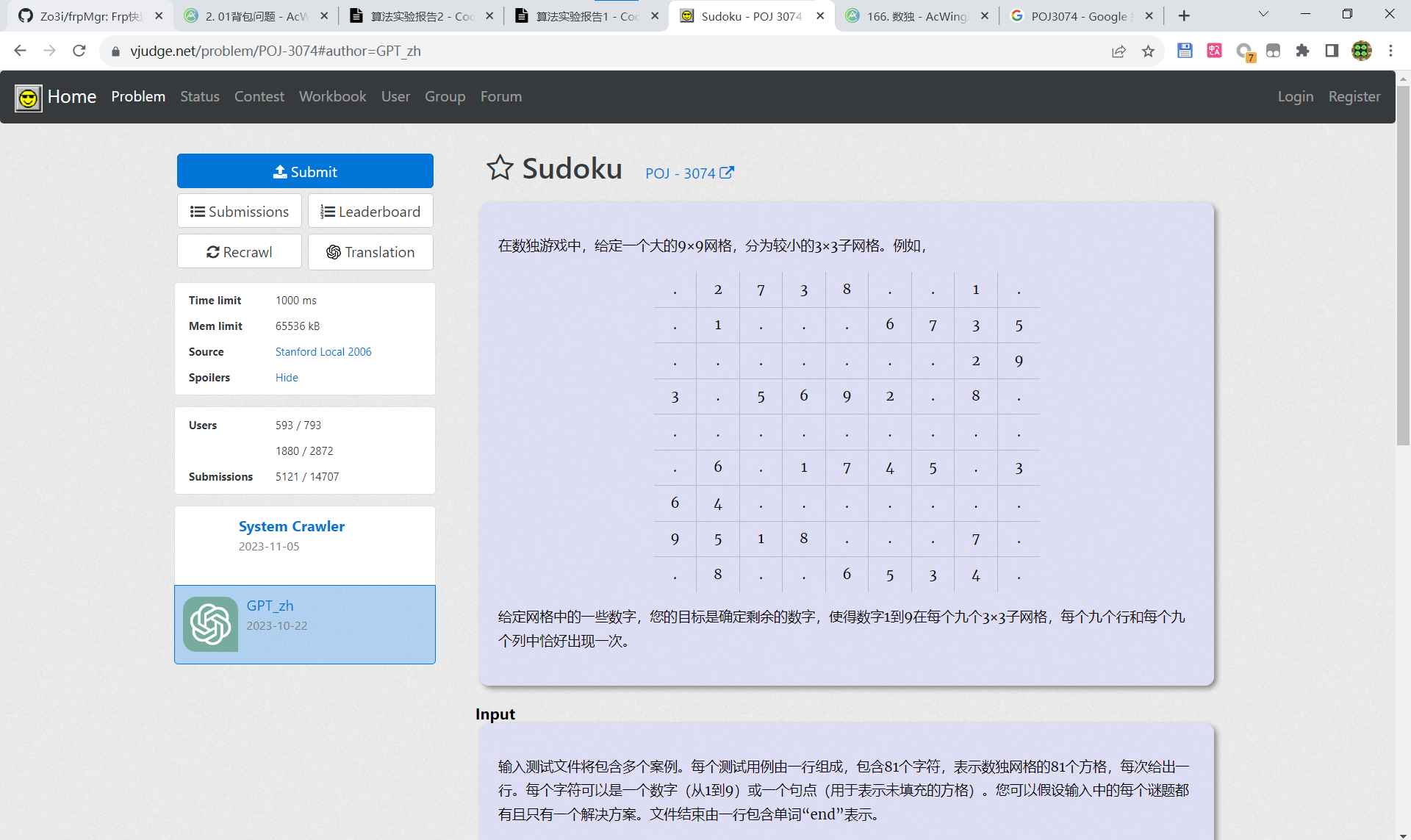
这里的输入:
1 | .2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534. |
其实还是跟八皇后类似
- 检查函数
- 枚举状态
- 剪枝(新增)
对于检查函数
- 检查当前行是否合法
- 检查当前列是否合法
- 斜行不需要检测,但是需要检查是否在当前九宫格内
1 | # 暴力检查,没有优化 |
然后是 DFS
1 | # 拆开 |

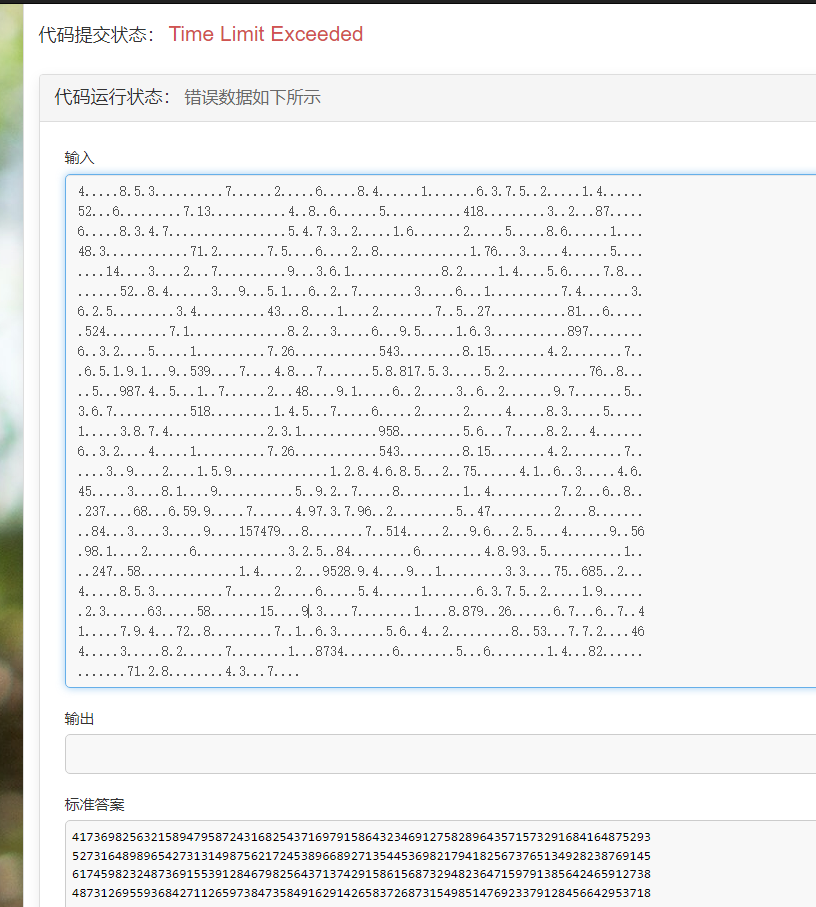
结果如图: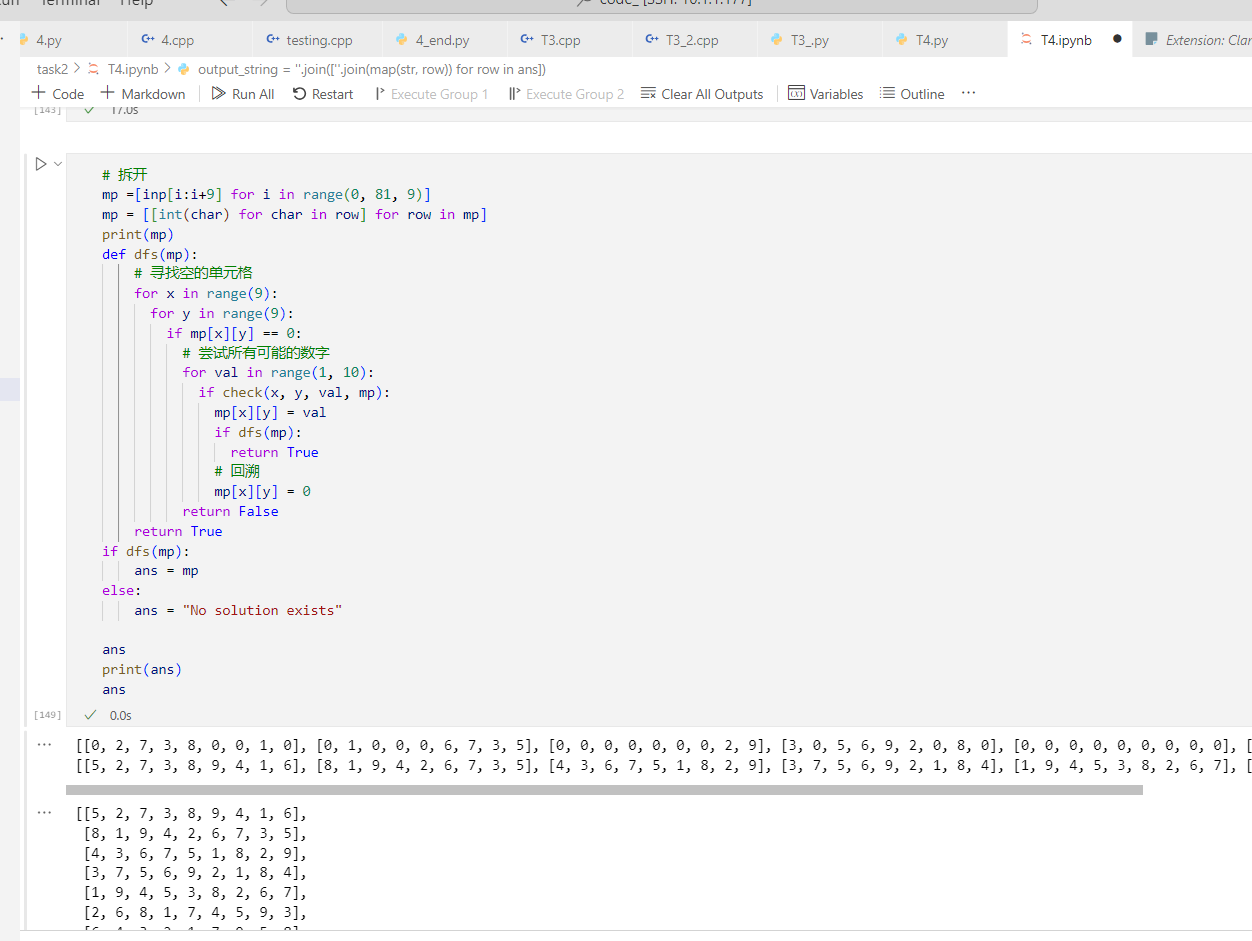
结果也正确: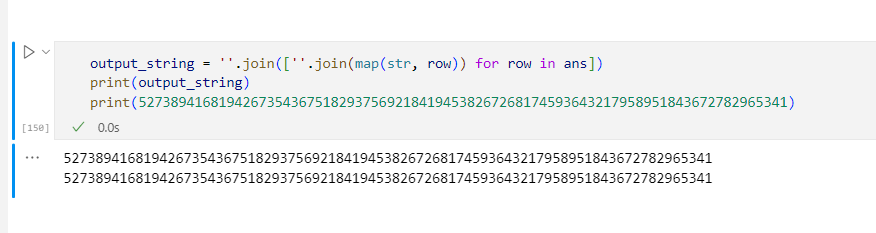
试试提交
很遗憾,Vjudge 不支持 Python
在 ACWing 上,虽然结果可以正确,但是样例都会 TLE
剪枝
- 选择下一个要填充的单元格时,优先选择候选数字最少的单元格。
check函数可以优化
有点难,这里就不再叙述啦。

时间复杂度
算法遍历数独的每一个空格,尝试填入数字(1-9),然后检查当前的填充是否合法。如果合法,则递归地继续填充下一个空格。如果不合法或者没有更多的空格可以填充,算法回溯并尝试下一个数字。最坏情况下的时间复杂度为 $O(9^m)$,其中 $m$ 是空白格子的数量。这是因为每个空格最多有9种可能的数字,而每次填充都需要递归地处理剩余的空格。
剪枝优化
剪枝操作不能改变算法的最坏情况时间复杂度(仍然是$O(9^m)$),但可以显著减少搜索空间和搜索步骤。
- 数独问题的解决是一个典型的搜索问题,其基本方法是回溯搜索。
- 最坏情况下的时间复杂度为 $O(9^m)$。
- 剪枝要用二进制优化,稍微有点复杂,这里不再详细描述啦。
二、总结
在本次算法实验中,我深入探讨了四个经典的算法问题:求幂集、N皇后问题、01背包问题和数独问题。通过这些问题的分析和解决,我获得了宝贵的编程经验和算法知识。
1. 求幂集
- 我学习了两种方法来解决幂集问题:深度优先搜索(DFS)和位运算。
- DFS方法的时间复杂度是 $O(2^N)$,而位运算方法的时间复杂度是 $O(N \times 2^N)$。
- 我了解到在不同情境下选择合适的算法对解决问题的效率有重要影响。
2. N皇后问题
- 通过递归和非递归的回溯法解决了N皇后问题。
- 两种方法的时间复杂度都近似于 $O(N!)$,但是由于约束条件的存在,实际上通常会更低。
- 我掌握了如何利用回溯法解决复杂的搜索问题,并了解了递归与非递归方法在实现上的差异。
3. 01背包问题
- 通过动态规划(DP)的方法解决了01背包问题,并学习了状态压缩的技巧。
- DP的时间复杂度为 $O(NW)$,通过状态压缩后,空间复杂度降低到 $O(W)$。
- 我深入理解了动态规划的思想,特别是如何定义状态和状态转移方程,以及如何优化空间复杂度。
4. 数独问题
- 利用回溯法解决了数独问题,并尝试了优化搜索的剪枝技巧。
- 回溯法的时间复杂度为 $O(9^m)$,其中 $m$ 为空白格子的数量。
- 我学习到了如何应用回溯法解决实际的逻辑填充问题,并意识到了优化搜索过程中的重要性。
综合体会
通过实际编写代码和解决问题,我更加清楚地认识到算法在解决复杂问题中的重要性。特别是在面对较大的数据集时,选择一个高效的算法是非常关键的。在未来的学习和职业生涯中,我需要持续关注并学习更多高效的算法,以便能够更好地应对各种挑战。